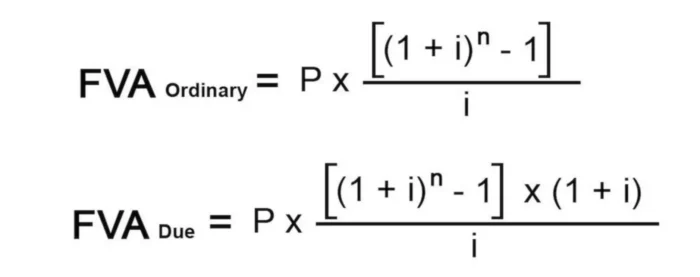Value of Money
Financial management requires the constant implementation of various calculations related to cash flows in different periods of time. Estimating the value of money over time plays a key role in these calculations. Its essence is that the value of money changes over time.
The concept of the change in the value of money over time plays a central role in the practice of financial calculations and expresses the need to take into account the time factor in the implementation of long-term financial transactions by assessing and comparing the value of money when a project is started and when investment is returned in the form of cash generated in the future.
This concept states that the value of money changes over time, taking into account the rate of return, which is usually the interest rate. Thus, the same amount of money in different periods of time has a different value. Moreover, the value of money is always higher now than in any future period. This difference is determined by the effect of inflation, the risk of not receiving income when investing capital, and other factors.
As you know, inflationary processes inherent in any economy cause the depreciation of money. This means that the monetary unit has a higher value today than tomorrow. This determines the desire to invest money in order to at least receive income that covers losses due to inflation. In any financial transaction, there is also a risk of non-return of the invested funds and/or non-receipt of income.
Future Value of an Annuity
In financial transactions, contracts sometimes provide for a series (flow) of payments (debt repayment), all elements of which are positive values, and the intervals between successive payments are constant. This stream of payments is also defined as a financial annuity.
Accordingly, the definition of an annuity is payments received at regular intervals over a specified period. If receipts occur at the beginning of the period, you would see it referred to as annuity due. This is what sets it apart from the more common ordinary annuity, where the next sum of money is paid at the end of the period.
An annuity is one of the key concepts in financial and commercial calculations. The logic of the annuity payment scheme is widely used in investment planning, investment analysis, valuation of debt and equity securities, and others.
It is assumed that the payments received are immediately invested at a certain percentage, and at the end of the investment period, the procedure is repeated. The total amount of all receipts with interest accrued on them at the time of the expiration of the annuity is the accumulated amount or the future value of an annuity. This is the amount of funds invested at the moment that they will turn into after a certain time passes, taking into account the interest rate.
Formula and Example
As you can see from the illustration above, you will need to use a different formula depending on the type of annuity you wish to calculate. In both cases, the required input variables are the same.
Ordinary annuity
A student decides to deposit $200 every month into their bank account to save money for graduate school. The bank will pay 6.5% interest compounded monthly. How much money is he going to have in their bank at the end of 5 years? Assuming that this individual makes payments on the 31st of every month, we are going to use the ordinary annuity equation.
Before you can actually input the variables into the formula, you need to find the interest rate for each month by turning the percentage into a decimal format and dividing by 12 months or 0.065 divided by 12. This will give you a monthly interest rate of 0.00542. Now, you just need to input all the other numbers into the formula. As a result, you will get $14,134.79 at the end of the 5 years. What this means is that if you deposited $200 every month into an account that paid 6.5% interest compounded monthly for 5 years, you would have $14,134.79 on your balance.
Annuity due
Now, let’s look at an example where deposits or payments are done on the first of each month or beginning of any other period. Let’s say you want to save some money while you are still working, so you have additional money to use when you no longer be able to work. So, once every year you go to your bank and deposit $1,000 at the beginning of each year. The interest rate is 5% compounded yearly. How much will you have available in your bank account after 18 years pass?
Looking at the formula represented below, you will input $1,000 for P. Since you are depositing on yearly basis, you do not need to do anything with the interest rate other than converting it into a decimal format, which will give you 0.05. For n, you will input 18 years.
Now, you will basically fill in the formula and just do a little bit of arithmetic or use a calculator. After 18 years, you will have $29,539 in the bank. Your total investment was really 18 years x $1,000 or $18,000. Your money has been at work all these years and has made you additional income. Plus, you did not fill a huge financial burden by making small deposits.